Using some assumptions driven from recent data and current response rate, I have built a fairly simple model to predict the number of COVID-19 cases that will be seen in the U.S.
The model starts with Seattle which reported its first case around Jan 21st. It didn’t go into an emergency state till the end of February.
The model assumes an average rate of infection after the average incubation period. It also assumes a ratio of local infection and infections that travel to other areas. This leads to the model’s idea of clusters. When an infection travels to another area, it creates a cluster. In a cluster, once a certain number of cases are detected, the area typically goes into a state of lockdown and emergency. The result of this should be a quickly declining spread and stopping of creating of additional clusters. The model assumes a more and more aggressive reaction response, based on recent data where some places when into emergency or lockdown mode after just 4 reported cases.
The further modeling of areas that are in actual or virtual lockdown is the difficult part as there is no clear data on how quickly the spread will stop.
The model shows that currently there are close to 19,000 people in the US that are already infected. Most of them were infected in the 1st week of March and thus are starting to show symptoms now. Thus over the next week or so, the number or confirmed cases will rise dramatically from the last reported 2500 or so.
The model estimates that the total number of infected cases will rise to somewhere between 22,000-25,000 after which the transmission will slow down significantly and essentially be contained. It is estimated that this will happen around the second week of April.
Below is a graph of the estimate from the model.
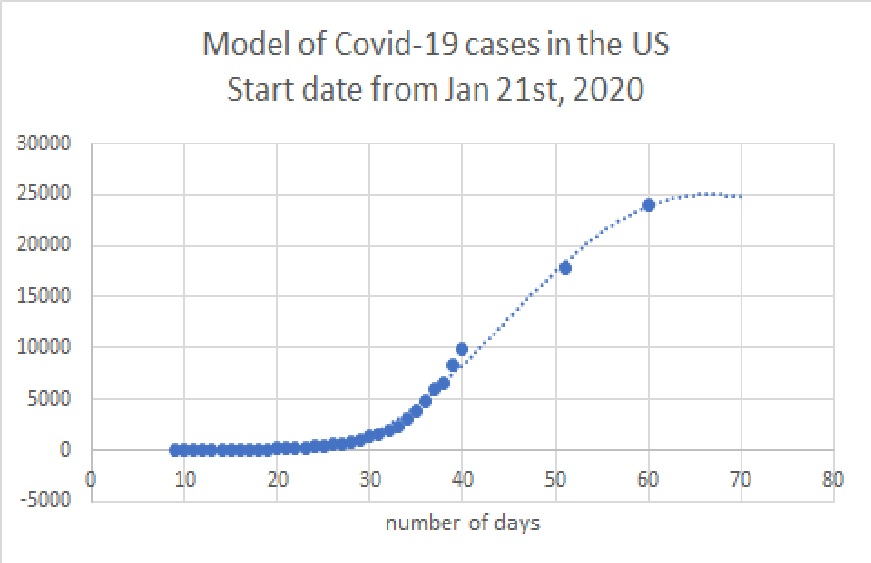
Of course, no one knows exactly what will happen. The model was built was a rather simple, but logical, set of assumptions and was driven by observed data so far in the US and other countries, but this data is what I found on the internet, which in itself is a bit flawed.







